Github链接

本页面内容由tex转换而来，但看上去显示问题似乎多多，更推荐阅读此PDF版本

动力系统与Julia集

在数学中，动力系统是一个重要的研究领域，关注系统状态随时间变化的行为。动力系统可以理解为一条规则，系统的每个状态会在这条规则下发生变化。通过不断重复这个规则，我们可以揭示系统内部潜在的模式和结构。当这一思想应用于复数平面时，就进入了一个充满几何美感的领域，即复动力系统。而在复动力系统中，Julia 集、Fatou 集 和 Mandelbrot 集 是三个经典的研究对象，它们为我们展示了复平面上的一个简单结构居然能生成无比复杂的结构与迷人的图形。

动力系统与复平面

在复动力系统中，我们通常研究一个复变量的映射 $f(z)$，它将复数 $z$ 映射到新的复数值。 在本文中，我们将考察 映射 $f(z) = z^m + c$，其中$m\ge 2, m \in \mathbb{N}$, $c$ 是一个复常数。对于给定的初始点 $z_0$，我们可以不断应用规则

$$z_{k+1} = f(z_k)$$

生成一个复数序列，即

$$\begin{aligned} z_0 & , \\ z_1 & = f(z_0), \\ z_2 & = f(z_1) = f(f(z_0)) = f\circ f(z_0), \\ z_3 & = f(z_2) = f(f(f(z_0))) = f\circ f \circ f(z_0), \\ & \vdots \\ z_{k+1} & = f(z_k) = \underbrace{f\circ f \circ \cdots \circ f}_{k\text{个}f}(z_0) \end{aligned}$$

这里使用了记号

::: definition 定义 1.

$$f \circ g(\;\cdot\;) \overset{\mathrm {def} }{{}={}}f(g(\; \cdot\; )).$$

:::

在给定一个$z_0$后，我们自然会想考察$\lim_{k\to\infty} z_k$的敛散性。

Gaston Julia 和 Benoît Mandelbrot 的研究

Julia 集得名于法国数学家 加斯顿·朱利亚（Gaston Julia），他在20世纪初研究了这些集合的性质，并在1918年发表了经典论文" Mémoire sur l'itération des fonctions rationnelles"(有理函数迭代论文)。20世纪后半叶，伯努瓦·曼德布罗（Benoit Mandelbrot）在计算机的帮助下，系统地研究了 Mandelbrot 集，这个集合也因此由他命名，开启了分形几何学的新篇章。通过计算机的图像展示，Mandelbrot 集的复杂边界和自相似性得以被人们直观理解，也让 Julia 集和 Mandelbrot 集在视觉艺术中广受欢迎。

发散、不发散与 Julia 集

在上述迭代过程中，复动力系统的行为主要分为两种情况：一部分点会迅速发散，即随着迭代次数增加，其值趋向无穷远。而另一部分点则始终限制在一定范围内，不发散，而是在一个固定区域内循环或收敛到一个点。 根据这个区别，我们将这些点分类为不同的集合。

Filled Julia 集

Filled Julia 集（填充 Julia 集）是指经过无穷次迭代后在复平面上所有不发散点的集合。对于给定的映射 $f(z) = z^2 + c$，$c$是一个固定的复常数。 若经过无穷次迭代后该点不发散，则 $z_0$ 属于 Filled Julia 集；反之，则 $z_0$ 不在其中。Filled Julia 集在复平面上形成了一个闭合的区域，其边界的形状取决于常数 $c$ 的选择。

::: definition 定义 2. 关于多项式$f$的 filled Julia 集$K(f)$

$${\displaystyle K(f) \overset{\mathrm {def} }{{}={}}\left\{z\in \mathbb {C} \mid f^{k}(z)\not \to \infty ~{\text{as}}~k\to \infty \right\}}.$$

:::

这里的$f^n(z)$与通常所指不同：

::: definition 定义 3.

$$f^n(\;\cdot\;) \overset{\mathrm {def} }{{}={}}\underbrace{f\circ f \circ \cdots \circ f}_{n\text{个}f}(\;\cdot\;).$$

:::

Fatou 集

与 Filled Julia 集互补的是 Fatou 集，它是复平面上所有初始点轨迹趋向稳定的区域。Fatou 集中的点在迭代过程中收敛某个固定点或周期循环。

::: definition 定义 4.

$$F = \hat{\mathbb{C}}\setminus J.$$

:::

Julia 集：Filled Julia 集的边界

Julia 集定义为 Filled Julia 集的边界，是那些"临界"点的集合，位于发散点和不发散点之间。与 Fatou 集的平滑性质不同，Julia 集的结构非常复杂，具有极高的细节和不规则性和非整数维数。Julia 集表现出明显的自相似性：无论如何放大，局部结构都会与整体相似，呈现出分形特征。

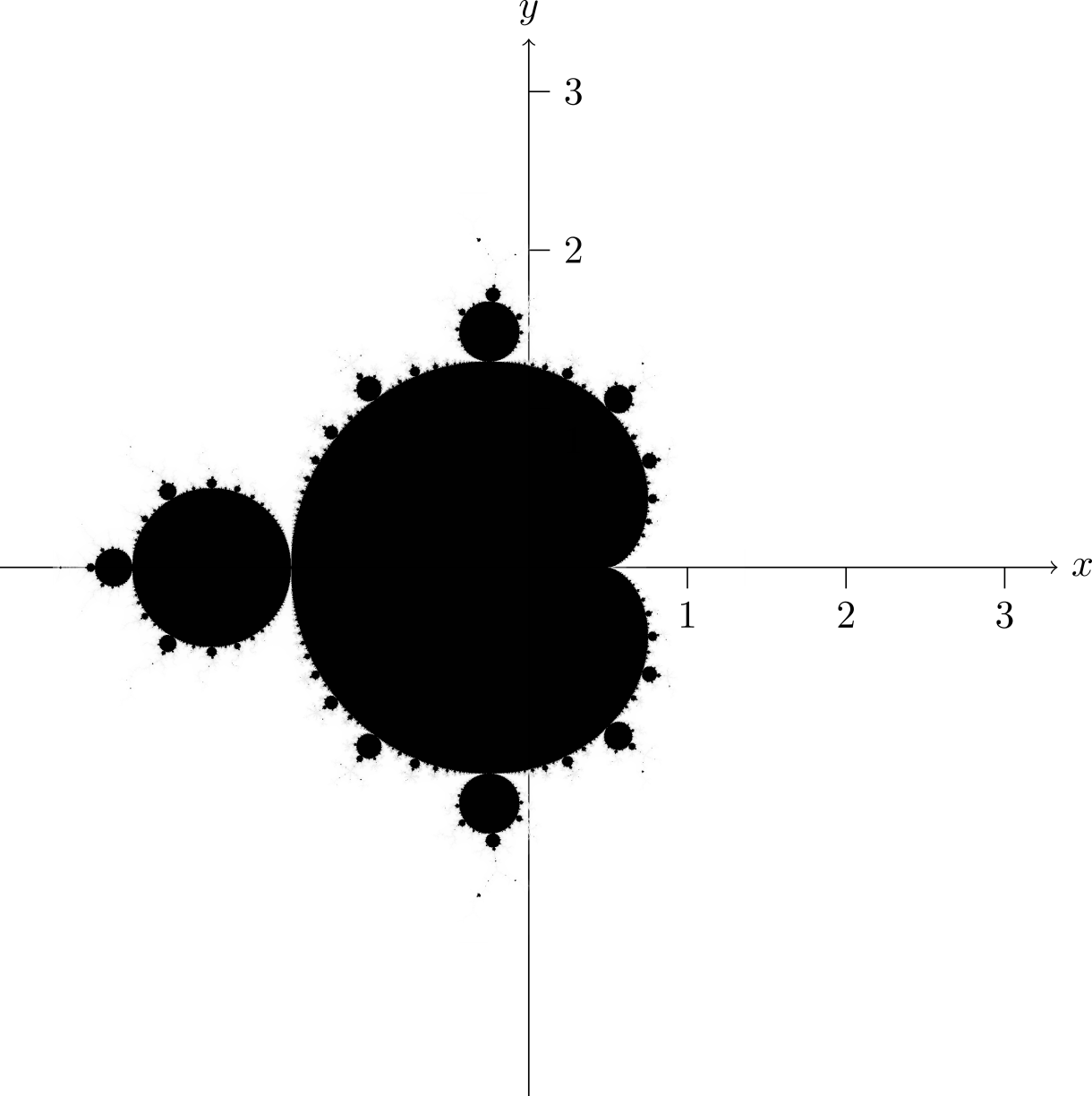
Mandelbrot 集，它与 Julia 集的关系

Mandelbrot 集（黑色区域）是 Julia 集的另一种表现形式。我们定义 Mandelbrot 集为复平面上所有使得初始值 $z_0 = 0$ 的级数在 $z_{k+1} = f(z_k) = z_k^2 + c$ 的迭代下不发散的参数 $c$ 的集合。

::: definition 定义 5.

$$\text{Mandelbrot 集} = \{c \mid f^k(z) \not\to \infty\ \text{as}\ k \to\infty \}$$

:::

因此，可以将 Mandelbrot 集看作 Julia 集的"地图"，它记录了每个 $c$ 值生成的 Julia 集的连通性信息。Mandelbrot 集的形状独特，具有复杂的边界和丰富的分形结构，与 Julia 集一样展示出自相似性。

Julia集的计算机绘制

理论基础

借助计算机，我们可以对复平面上的每个点逐一进行迭代，判断它们是否发散，并将这些信息以颜色表示出来，生成 Julia 集的图像。 使我们得以直观感受到这一分形世界的无限美感。

我们需要以下定理来保证绘图的准确性。

::: {#判断法 .theorem} 定理 1. 对 $f(z) = z^2 + c$ 满足 $c\in\mathbb{C}$ 且 $|c|<2$, 若存在$k$使得$z_k = f(z_{k-1})$， $|z_k|>2$，则$\lim_{n\to\infty} f^n(z_0) = \infty$, $\forall z_0 \in \mathbb{C}$. :::

::: proof Proof. 记 $z_{k+1} = f(z_k) = z^2_{k} +c$, $|z_k|>2$. 记 $\delta_k = |z_k| - 2 > 0$, 则

$$|z_{k+1}| = |z_k^2 + c| \ge |z_k|^2 - |c| = 4 + 4 \delta_k + \delta^2_k - |c| = (4+\delta_k)\delta_k + 4 - |c| > 4 \delta_k + 2 = 3 \delta_k + |z_k|.$$

由上式，当 $n>k$, 有 $\delta_{n+1} = |z_{n+1}| - 2 > 4 \delta_n > \delta_n$, 从而

$$\lim_{n\to\infty} |z_n| = \lim_{n\to\infty}\left( \sum_{i=k}^n |z_{i+1}| - |z_i |\right) + |z_k| > \lim_{n\to\infty}\left( \sum_{i=k}^n 3 \delta_i \right) + |z_k| > \lim_{n\to\infty}\left( n-k \right) \cdot 3 \delta_k + |z_k| = \infty.$$

◻ :::

::: {#高阶情形 .corollary} 推论 1. 对 ,$f(z) = z^m + c$ 满足 $m\in \mathbb{N}$ , $m\ge 2$ , $c\in\mathbb{C}$且$|c|<2$, 若存在$k$使得$z_k = f(z_{k-1})$， $|z_k|>2$，则 $\lim_{n\to\infty} f^n(z_0) = \infty$, $\forall z_0 \in \mathbb{C}$. :::

::: proof Proof. 只需注意到当 $|z_k|>2$ 且 $m\ge 2$时，$|z_k|^m \ge |z_k|^2$, 再由定理1即得. ◻ :::

计算机绘制逻辑

有了定理1{reference-type="ref" reference="判断法"}，我们便可以在计算机中通过以下方法画出一个近似的Julia集：

1. 在程序中创建一个数组来存储每个像素的迭代结果。该数组的大小与图像的分辨率相同，每个元素将存储该点在计算过程中迭代次数。 对于图像中的每个像素位置 $(i, j)$，我们将其线性地映射在复平面上的坐标 $z_0 = x + y\mathrm{i}$, $x \in[x_{\text{min}}, x_{\text{max}}],\ y\in[y_{\text{min}}, y_{\text{max}}]$ 。
2. 对于每个复数点 $z_0$，使用最大迭代次数的限制来判断该点是否发散。从 $z_0$ 开始迭代，按照公式 $z_{k+1} = z_k^2 + c$ 不断更新 $z$ 的值。迭代的过程中：
   • 如果 $z_k$ 的模，即 $|z_k|$，在某次迭代中超过2，则根据定理1便可知该点是发散的，停止迭代。
   • 如果在最大迭代次数内 $|z_k|$ 从未超过 2，则该点被认为不发散，即属于 Filled Julia 集。

根据以上方法， 我们便可以使用C++编写代码实现Julia 集的绘制了。

为生成的图像着色

为了更直观地展示 Julia 集图像，可以使用每个点的迭代次数为其着色。 让发散区域和不发散区域的颜色差异突显出 Julia 集边界的复杂性和分形特性，使得图像充满视觉美感。 为此，我们引入颜色映射函数的概念。

• 颜色映射函数的主要任务是将一组数值（例如温度、压力、密度等）转化为对应的颜色。这种转换使得复杂的数据能够通过颜色的变化被直观地呈现出来，便于观察和分析。
• 根据数据的特点和展示需求，设计一个颜色梯度。例如，从冷到热、从低到高、从浅到深等。常见的颜色梯度包括蓝色到红色、绿色到黄色等。这些渐变色可以帮助人们快速识别数据中的趋势和异常。
• 为了增强颜色的表现力，颜色映射函数常将数值范围划分为多个区间，每个区间内定义不同的颜色过渡方式。这种分段过渡使得颜色变化更加平滑和连贯，同时也能突出特定区间内的数据特征。

一个经典的颜色映射Jet

Jet颜色映射是一种广泛应用于科学数据可视化的彩虹色谱映射函数，最初由MATLAB引入。它将标量数据值映射到从蓝色到红色的连续颜色梯度，具体颜色顺序通常为蓝色、青色、绿色、黄色和红色。Jet颜色映射因其直观的色彩过渡和高对比度，常用于显示温度分布、地形高度、流场等数据。然而，值得注意的是，Jet映射并非感知上均匀的色彩映射，可能会引入视觉伪影或误导性的信息，因此在某些应用中需谨慎使用。

Jet颜色映射函数通常定义在闭区间 $[0, 1]$ 上，将输入标量 $t$ 映射到RGB颜色空间中的红色（R）、绿色（G）和蓝色（B）分量。

$$\begin{bmatrix} R(t) \\ G(t) \\ B(t) \end{bmatrix} = \begin{bmatrix} \text{clamp}(1.5 - |4t - 3|, \ 0, \ 1) \\ \text{clamp}(1.5 - |4t - 2|, \ 0, \ 1) \\ \text{clamp}(1.5 - |4t - 1|, \ 0, \ 1) \end{bmatrix}$$

其中，函数 $\text{clamp}(a, \ 0, \ 1)$ 将值 $a$ 限制在区间 $[0, 1]$ 内，即：

$$\text{clamp}(a, \ 0, \ 1) = \begin{cases} 0, & a < 0, \\ a, & 0 \leq a \leq 1, \\ 1, & a > 1. \end{cases}$$

2024年12月15日 一个课程作业